Nedenfor er forklart noen sentrale definisjoner innen støy på en enkel og litt mer teknisk måte.
(Siden er under utvikling og vil bli drøftet med deltagere på NYF-YE-03 29. februar 2024.)
Lyd er vibrasjoner som beveger seg gjennom et medium (som luft, vann, eller faste stoffer) i form av lydbølger. Disse bølgene har to primære egenskaper som påvirker hvordan vi oppfatter lyd: amplitude og frekvens. Amplitude er relatert til lydbølgens styrke (energi), mens frekvens bestemmer tonens høyde.
Bølgelengde
Enkel forklaring: Bølgelengde er avstanden mellom to topper i en lydbølge (eller en hvilken som helst annen type bølge, som lys eller vannbølger). I mekanikk kan vi sammenligne dette med avstanden en pendel beveger seg fra det ene ytterpunktet til det andre før den svinger tilbake.
Teknisk forklaring: Bølgelengden av en lydbølge er den fysiske avstanden mellom to korresponderende punkter i påfølgende bølger, som to topper eller to bunner. Den er invers relatert til frekvensen av bølgen via forholdet ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


I figuren er bølgelengen angitt med L og amplituden med H.
Frekvens
Enkel forklaring: Frekvens beskriver hvor ofte bølgetopper passerer et fast punkt i løpet av et sekund. Det måles i Hertz (Hz). Det er som å telle hvor mange ganger en pendel svinger frem og tilbake hvert sekund. Høyere frekvens betyr at bølgene passerer oftere, som en pendel som svinger raskere.
Teknisk forklaring: Frekvens, målt i Hertz (Hz), representerer antall sykluser en bølge fullfører per sekund. I akustikk refererer det spesifikt til antall trykkvariasjoner per sekund som en lydbølge genererer. For lydbølger er frekvensen det som bestemmer tonens høyde.
Desibel (dB)
Enkel forklaring: Desibel er en enhet som brukes til å måle lydens intensitet eller lydtrykk. Du kan tenke på det som en måte å fortelle hvor høyt eller kraftig en lyd er. I mekanikk kan det sammenlignes med hvordan man måler hvor tung noe er, for eksempel i kilogram. Jo flere kilogram, desto tyngre er gjenstanden. På samme måte indikerer høyere decibel en kraftigere lyd.
Teknisk forklaring: Desibel er en logaritmisk enhet som brukes til å uttrykke forholdet mellom to verdier av en fysisk kvantitet, oftest intensitet eller kraft.
(1) ![]()
![]()
Lydtrykk (p)
Dette logaritmiske målet gjør det mulig for oss å håndtere det ekstremt brede området knyttet til ulike fysiske størrelser. Det brukes bl.a til å beskrive lydtrykknivå (SPL), lydintensitet og lydeffektnivå, hvor 0 dB representerer et referansenivå. Bruk av logaritmer betyr også at regnereglene blir annerledes (se nedenfor).
Enkel forklaring: Lydtrykk er en måling av trykkvariasjonen i luften som skyldes en lydbølge. Det er som å føle vinden mot ansiktet ditt; sterkere vind (eller lydbølger) gir et høyere trykk.
Teknisk forklaring: Lydtrykk (p) eller lydstyrke er den lokale trykkvariasjonen fra det gjennomsnittlige atmosfæriske trykket, forårsaket av passering av en lydbølge. Det er kvantifiserbar som den øyeblikkelige forskjellen fra det atmosfæriske trykket og er proporsjonal med bølgens amplituden. Lydtrykknivå (![]()
![]()
(2) 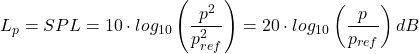
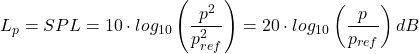
, hvor ![]()
![]()
Dette logaritmiske målet gjør det mulig for oss å håndtere det ekstremt brede området av lydintensiteter mennesket kan oppfatte. Bruk av logaritmer betyr også at regnereglene blir annerledes. En dobling av lydtrykknivået, uansett om det er fra 40 dB eller 90 dB, så er dette hhv. 43 eller 93 dB.


Lydeffekt (w)
Enkel forklaring: Lydeffekt (w) er mengden energi en lydkilde sender ut i form av lyd per tidsenhet, målt i watt (W). I mekanikk er dette som kraften som blir brukt når du gjør et arbeid, for eksempel når du skyver en kasse over gulvet. Mer kraft betyr mer arbeid blir gjort, og på samme måte betyr mer lydeffekt at det sendes ut mer lydenergi.
Teknisk forklaring: Lydeffekt er den totale energien som lydbølgen overfører per tidsenhet gjennom en flate, og er en indikator på lydkildens totale akustiske utstråling. Den måles i watt (W) og er direkte relatert til både lydtrykket og arealet lyden passerer gjennom. Kilder avgir en effekt målt i Watt og lydeffektnivået (![]()
![]()
![]()
![]()
Lydintensitet (I)
Enkel forklaring: Lydintensitet er mengden lydenergi som passerer gjennom et område på en bestemt tid. Dette kan sammenlignes med hvor mye arbeid som blir gjort i et bestemt område i mekanikk. Hvis du bruker mer kraft over det samme området, sier vi at arbeidsintensiteten øker.
Teknisk forklaring: Lydintensitet er et mål på lydens kraft per enhetsareal, i retning av bølgepropagasjon. Det er en vektorstørrelse som er direkte proporsjonal med både kvadratet av lydtrykket og partikkelhastigheten i mediet. Lydintensitet er ofte uttrykt i watt per kvadratmeter (W/m²) og lydintensitetsnivpet (![]()
![]()
![]()
![]()
Loudness
Mens desibel måler den fysiske intensiteten av lyden, refererer “loudness” til den subjektive opplevelsen av lydens styrke. Loudness er ikke bare avhengig av lydens intensitet (dB), men også av dens frekvens, varighet, og lytterens hørselskarakteristikker. Psykoakustikk er studiet av hvordan vi oppfatter lyd og måles i “phon”. 40 phon er hvordan et lydtrykknivå på 40 dB av en ren tone ved 1000 Hz oppleves av unge personer uten hørselsskade. Denne kurven antas å ha dannet utgangspunktet for veiekurven som vi bruker for å beregne lydtrykknivå i dB(A). Den nederste kurven ![]()
![]()


Veiekurver
Enkel forklaring: Veiekurver er grafer som viser hvordan ørets følsomhet for lyd endrer seg med forskjellige frekvenser. I mekanikk kan dette sammenlignes med hvordan forskjellige materialer kan bære forskjellige vekter før de bøyer seg. På samme måte kan øret “bære” eller oppfatte forskjellige lydfrekvenser på forskjellige måter.
Teknisk forklaring: Veiekurvene er et resultat av psykoakustiske eksperimenter som illustrerer vår opplevelse av lyd ved ved forskjellige frekvenser. Disse kurvene viser SPL ved forskjellige frekvenser som oppfattes som like høye av et gjennomsnittlig ungt menneske (se Loudness). I dag benyttes i praksis kun veiekurve A og C.


Det er viktig å merke seg at veiekurvene ikke sier noe om hvor lett hørselen vår blir skadet, men hvordan vi oppfatter lydtrykknivået ved ulike frekvenser.
Ekvivalentnivå (Leq)
Enkel forklaring: Ekvivalentnivå er en måte å måle gjennomsnittlig lydnivå over tid. Dette kan sammenlignes med å finne gjennomsnittshastigheten til en bil som endrer hastighet over en lang kjøretur.
Teknisk forklaring: Ekvivalentnivået ![]()
![]()
(3) ![]()
![]()
, hvor ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Et ekvivalent nivå kan angis for en bestemt periode f.eks. 8 timer. Dette angis da ![]()
![]()
![]()
![]()
Hvordan regne med desibel
Desibel (dB) er en logaritmisk enhet som brukes til å måle forholdet mellom to fysiske størrelser. Når vi jobber med desibel, er det viktig å huske på at vi bruker en logaritmisk skala fordi det menneskelige øret oppfatter lyd på en logaritmisk måte, ikke lineært.
Eksempelvis vil summen av to like lydtrykknivåer tilsvare et tillegg på 3 dB uansett hvilke to lydtrykknivåer vi legger sammen: 0dB + 0dB = 3dB, 80dB + 80dB = 83dB osv. Er det 6 dB forskjell mellom de to lydtrykknivåene du skal legge sammen skal du kun legge til 1dB til den høyeste verdien: 0 dB + 6dB = 7dB, 86dB+80dB=87dB, osv. Du kan beregne dette ved å bruke formel 4 eller ved å bruke figuren nedenfor.
(4) ![]()
![]()


Referanser
Pettersen, O. K. (2000). Lyd og støydemping. Akustisk grunnlag. Trondheim, SINTEF.
Standard Norge (2023). Acoustics — Normal equal-loudness-level contours, Standard Norge. ISO 226.


